Hábitos compostos, resultados exponenciais

"Os juros compostos são a oitava maravilha do mundo. Aquele que entende, ganha. Aquele que não entende, paga." -- (supostamente) Albert Einstein

Quando penso em juros compostos, a primeira imagem que me vem à mente é a de uma curva exponencial, representando uma quantia de dinheiro investida crescendo, como uma bola de neve, com o passar do tempo.

Acredito que essa seja a imagem que aparece de imediato para a maioria das pessoas, uma vez que é fácil entender os efeitos dos juros compostos quando o assunto é dinheiro.

Porém, ultimamente, venho pensando bastante a respeito da influência de dinâmicas semelhantes a dos juros compostos nas mais diversas áreas da nossa vida: na saúde, nos estudos, no trabalho, na felicidade etc.

Por mais que acredite firmemente que dinâmicas análogas rejam essas outras áreas, a extrapolação da ideia a partir do seu sentido convencional não é tão trivial.

Primeiro, porque acredito que nós não lidamos muito bem, em um nível intuitivo, com crescimentos não lineares. Segundo, porque nem todas as áreas são facilmente mensuráveis como o dinheiro. Você consegue ver claramente os números que representam o dinheiro alocado em um bom investimento crescendo, mas como você sabe que está "exponencialmente" mais saudável, mais feliz ou mais inteligente?

A consequência direta do nosso entendimento fraco dos efeitos de juros compostos fora das finanças é que acabamos não colhendo todos os frutos dessa oitava maravilha. Por definição, grande parte dos efeitos no cenário com juros compostos vem dos aportes iniciais, isto é, dos recursos alocados no início, uma vez que são essas alocações as multiplicadas pelas maiores potências. Todavia, é difícil ter consistência e persistir em atividades para as quais só veremos efeitos décadas no futuro.

Neste texto, vou explorar um pouco essa ideia. Escrevi o texto principalmente para ter mais clareza a respeito dos fatos, mas acredito que você consiga extrair ideias interessantes que se apliquem a sua vida. Se você já entende bem como funcionam os juros compostos, pode pular a próxima seção.

Juros compostos

Antes de transferir a ideia de juros compostos para outras áreas, acredito que seja importante explorar um pouco mais a fundo as suas implicações no contexto original, isto é, nas finanças. Por mais que a suposta frase de Einstein tenha sido praticamente incorporada ao senso comum, acho que muitas pessoas não entendem a fundo todas as suas consequências (eu certamente era uma dessas pessoas, antes de colocar os números no papel pela primeira vez).

Os juros compostos ilustram bem a regra de Pareto (também conhecida como regra do 80-20), que é outra relação que acredito ter mais profundidade do que o senso comum atribui.

Primeiro, a regra do 80-20 diz que 80% dos resultados (ou efeitos) são produzidos por 20% do esforço (ou das causas). Existem vários fenômenos que ilustram bem essa relação e os juros compostos são um deles.

Para explicar como funcionam os juros compostos, vou usar o exemplo dado pelo Fábio Holder neste vídeo.

Imagine que você consiga poupar R$ 1000,00 todos os meses e suponha também que você aloca esse dinheiro em um investimento que renda 1% ao mês. Suponha que você faça isso por 50 anos.

Qual o patrimônio acumulado ao final desse período?

Se você faz isso por 50 anos, você terminará com um patrimônio em torno de R$ 39.500.000,00.

O valor final é muito maior do que intuitivamente esperaríamos. A pergunta que naturalmente surge, então, é como que os R$ 1000,00 mensais se transformaram nos milhões após 50 anos?

A resposta é: por meio dos juros compostos.

A ideia é bem simples. O seu primeiro aporte, isto é, os primeiros R$ 1000,00 investidos, após 1 mês aumenta em 1%, virando R$ 1010,00. Após o segundo mês, aumenta mais 1% em cima do novo valor, transformando-se em R$ 1020,10, e assim por diante. No final dos 50 anos (isto é, 600 meses depois), aqueles primeiros R$ 1000,00 viraram, aproximadamente, R$ 391.583,40 (basta calcular R$ 1000,00 x (1,01)^600).

Porém, esse valor é o resultado apenas do primeiro aporte. Na situação hipotética, em que os aportes acontecem mensalmente, temos ao final dos 50 anos:

Aporte do primeiro mês depois de 50 anos: R$ 1000,00 x (1,01)^600 = R$ 391.583,40
Aporte do segundo mês depois de 50 anos: R$ 1000,00 x (1,01)^599 = R$ 387.706,33
Aporte do terceiro mês depois de 50 anos: R$ 1000,00 x (1,01)^598 = R$ 383.867,66
...
Penúltimo aporte: R$ 1000,00 x (1,01) = R$ 1010,00
Último aporte (no mês final): R$ 1000,00

Somando todos os valores, chegamos aos (aproximadamente) R$ 39.500.000,00.

A análise é bem simplista e os números utilizados são ilustrativos para você entender a ideia. Não vou entrar no mérito do investimento em si e dizer se 1% ao mês é factível ou não, se R$ 1000,00 mensais é muito ou pouco, ou se 50 anos é tempo demais. A equação tem três variáveis: o valor dos aportes, a rentabilidade (o 1% ao mês) e o tempo. O tempo é a mais importante de todas, por ser a que aparece no expoente.

Não está sendo levado em conta a mudança do valor do dinheiro no tempo, por exemplo, por conta da inflação, mas também não é levado em conta que, provavelmente, o salário da pessoa aumenta com o tempo, fazendo com que sejam possíveis aportes cada vez maiores com o passar dos anos.

Para o que quero mostrar, é importante notar duas coisas.

A primeira é que o crescimento é não linear, então, no início, os resultados demoram para aparecer, mas, depois, crescem de forma cada vez mais rápida. A segunda é que fica claro que os aportes iniciais são os mais importantes, uma vez que são eles que são multiplicados pelas maiores potências. Por outro lado, os últimos aportes praticamente não fazem diferença no patrimônio acumulado.

A regra do 80-20 aparece no cenário anterior porque, aproximadamente, 80% do patrimônio total no final do período, vêm dos 20% aportes iniciais.

Isso significa que uma pessoa que simplesmente pare de fazer aportes depois de 10 anos (20% de 50 anos), termina o período de 50 anos com aproximadamente 80% do patrimônio da pessoa que fez o aporte pelos 50 anos.

Isso serve para enfatizar a importância dos aportes iniciais.

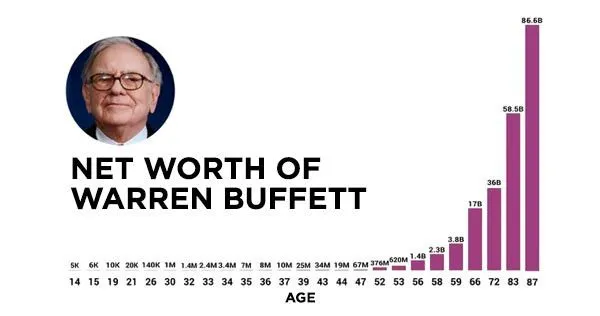
Só para concluir a ideia dos juros compostos nos investimentos, o gráfico abaixo representa o patrimônio do Warren Buffett, um dos homens mais ricos do mundo. Note que seu patrimônio aumentou significativamente no últimos anos, justamente por conta do efeito dos juros compostos.

(Fonte)

Hábitos compostos, resultados exponenciais

Eu acredito que os resultados em algumas áreas das nossas vidas crescem desproporcionalmente com o passar do tempo, desde que continuemos a fazer os aportes com a devida frequência. Além disso, à medida que o tempo passa, os resultados vêm de forma cada vez mais fácil.

O análogo dos aportes frequentes (que vão se acumulando para produzir os resultados) são os hábitos.

Uma das minhas experiências em particular me fez acreditar piamente nessa ideia. No meu caso, foram resultados acadêmicos produzidos pelo hábito de estudar.

Até um pouco antes do ensino médio, eu era um aluno mediano. Nunca tinha ficado de recuperação, mas também não tinha muitos pontos sobrando. Eu não me dedicava, porque as matérias não me interessavam e o meu desempenho acadêmico era reflexo direto da minha atitude.

Entretanto, quando estava prestes a começar o ensino médio, me contaram várias histórias de terror e o protagonista de todas elas era sempre o mesmo: o vestibular. Dessa forma, decidi que era hora de mudar a minha postura, levar a escola a sério e me preparar para o desafio que enfrentaria dali a 3 anos.

Me lembro nitidamente da tarde, depois do primeiro dia letivo, em que sentei para estudar a matéria que fora ensinada naquele dia. Repeti o processo nos próximos meses e, para a minha frustração, minhas notas eram praticamente iguais às que tirava nos anos anteriores, época em que eu mal abria o caderno.

Quando olhava para os lados e comparava o meu desempenho acadêmico com o dos meus amigos, não conseguia entender o que eu estava fazendo de errado. Claramente, muitos deles estudavam bem menos do que eu e, mesmo assim, tiravam notas muito mais altas que as minhas.

Por mais frustrante que era a situação, continuei estudando, simplesmente porque acreditava que era o que deveria fazer.

Em seis meses, minhas notas começaram a subir, embora lentamente. Em um ano, estava começando a ser reconhecido como um "bom aluno" e não mais como aquele esforçado, mas que não tem resultados tão bons. Em pouco mais de dois anos, estava consistentemente entre os melhores alunos do meu ano e passei no vestibular sem grandes dificuldades.

Evidentemente estava satisfeito por ter entrado na universidade e sentia um peso enorme sendo retirado das minhas costas. Porém, quando parei para refletir sobre o meu percurso, estava claro que, apesar de ser "um dos melhores alunos" do meu ano no ensino médio, não era "o melhor aluno".

Não que eu quisesse ser melhor que os outros, mas tinha o sentimento de que nessa diferença, havia uma lição importante escondida. O que me intrigava era o fato de que o conhecimento de alguns dos alunos que estavam na minha frente era muito, muito superior ao meu. Sentia também que, mesmo que eu me esforçasse tremendamente no curto prazo, não conseguia superá-los de forma alguma. Qual era o motivo dessa discrepância?

Conclui que o porquê da diferença eram os "aportes" iniciais.

Os alunos que estavam significativamente a minha frente sempre foram os melhores alunos. Sempre. Do maternal ao final do ensino médio. Há anos que eles estudavam e aprendiam bem, enquanto eu estava naquela jornada há menos de 3 anos. Consequentemente, o que eles aprenderam anos atrás sofreu a influência dos "juros compostos" para construir o conhecimento que eles tinham no presente.

Duas lições ficaram muito claras para mim naquele momento:

Não era o que eu fazia no presente que nos diferenciava e sim o que eu tinha deixado de fazer no passado. O conhecimento no presente era, na verdade, uma métrica "atrasada" do que tinha feito (ou deixado de fazer) no passado;
Era muito mais fácil evoluir nos estudos a partir do ponto que eu estava no final do ensino médio do que quando decidi começar a estudar. Os resultados estavam vindo de forma cada vez mais rápida. Na verdade, sentia inclusive que se parasse de estudar completamente por um tempo, o meu desempenho não cairia de imediato, por conta de todos os "resultados acumulados".

Quando comecei os estudos na universidade, já estava ciente da influência dos "juros compostos" nos estudos e tinha consciência de que as matérias de base (no caso de engenharia, as de matemática e física) eram fundamentais para construir os conhecimentos avançados. Estudei com afinco desde o primeiro dia, porque não queria chegar ao final da universidade, olhar para trás e pensar que havia aportes iniciais que eu tinha condições de fazer que potencializariam muito os meus resultados e que eu os tinha deixado passar.

Da primeira tarde, logo antes do início do ensino médio em que decidi sentar para estudar a matéria do dia até hoje (início de 2021) se passaram 11 anos.

Fui de um aluno mediano, para alguém que passou no vestibular antes de terminar o ensino médio, concluiu a graduação em menos de 5 anos e concluiu o mestrado em uma das 5 melhores universidades do mundo (a título de curiosidade, a mesma que Einstein, citado no início do post, estudou).

As magnitudes dessas conquistas acadêmicas, se pudessem ser mensuradas, seguiriam uma exponencial e o hábito responsável por conduzir os resultados foi o estudo.

Não falo isso de forma arrogante, a cada degrau que subi, encontrei pessoas muito melhores do que eu nas mais diversas esferas da vida e foram essas pessoas que me influenciaram e me motivaram a melhorar continuamente. Além disso, o mérito das conquistas não é todo meu. Sempre tive as habilidades, bem como a ajuda e a sorte para superar os obstáculos que encontrei.

Alguns, quando veem a minha trajetória, podem achar que eu sou "inteligente", porém sou essencialmente a mesma pessoa de 11 anos atrás e, naquela época, poucos me descreveriam dessa forma.

Qual é o próximo capítulo?

Já ouvi falar que a nossa vida é escrita em capítulos de 10 anos. Meus últimos 10 anos foram religiosamente dedicados a me desenvolver academicamente e, apesar de ter a oportunidade de continuar nessa direção (começar o PhD), quero mudar um pouco o rumo.

Eu gosto muito das ideias do Naval Ravikant. O Naval fala que, essencialmente, o objetivo da vida é ser feliz, saudável e rico, nessa ordem.

Já pensei bastante sobre cada uma dessas dimensões e o que cada uma delas representa para mim. Evidentemente, não tenho respostas concretas, mas enxergo cada uma como uma área digna de investimento para os próximos anos. Por mais abstratas que sejam essa áreas, existem hábitos e atividades concretos que se encaixam em cada uma delas que conduzem os resultados em uma mesma direção.

Por exemplo, para ser feliz, minhas expectativas devem estar alinhadas com a minha realidade; preciso cultivar boas relações com as pessoas à minha volta; preciso reservar um tempo para as atividades que eu mais gosto de fazer. Para ser saudável, preciso cuidar da minha saúde física e mental; preciso me exercitar, me alimentar bem e dormir bem. Para ter riqueza, preciso ganhar mais do que eu gasto; preciso investir bem; preciso gerar valor para a sociedade e capturar parte desse valor de volta; preciso ganhar dinheiro de formas que não estejam diretamente associadas com o meu tempo.

Vejo os resultados dentro de cada uma dessas áreas como uma exponencial e os hábitos são os responsáveis pelo progresso. Todos os dias, estou fazendo os meus aportes, por menores que sejam, confiando que daqui a 10 anos ou mais vou colher os frutos.

Os aportes (hábitos) iniciais, por mais que sejam os mais importantes, são os mais difíceis de serem feitos, exigindo disciplina para que ocorram consitentemente.

Isso porque, como disse, o valor de qualquer métrica no presente é um indicativo do que você fez no passado e não do que você está fazendo agora. Por exemplo, na área da saúde, as suas taxas nos exames de sangue ou a sua forma física hoje não são consequência do que você fez hoje pela manhã ou do que você fez nas últimas 2 semanas; elas são reflexo dos seus hábitos nos últimos anos. O corolário é que os resultados não aparecem de imediato. O início de um crescimento exponencial é lento, mais lento que um crescimento linear comparável.

Por fim, gostaria de responder a duas questões que você talvez esteja levantando.

A primeira é que você pode estar pensando que 10 anos é muito tempo. A minha resposta é: sim, é bastante tempo mesmo, mas os 10 anos vão passar de qualquer forma, então é melhor que você passe fazendo alguma coisa.

A segunda é que você pode estar achando que é tarde demais para começar. Para isso, trago o ditado que diz que "o melhor momento para se plantar uma árvore foi a 10 anos atrás. O segundo melhor momento é agora".