On neural machine translation and emotion recognition

Overview

The problem of translation can be seen as the problem of modeling the conditional probability distribution $p(y | x)$  of translating a source sentence $(x_1, \dots, x_n)$ into a target sentence $(y_1, \dots, y_m)$ .

One of the most popular neural machine translation (NMT) approaches is based on an encoder-decoder architecture. The encoder receives a source sentence as its input and is responsible for generating a representation for that sentence. The decoder, then, generates one target word at a time based on the representation provided by the encoder.

For instance, one could choose one recurrent neural network (RNN) for the encoder and another for the decoder. The step-by-step of such an NMT model would be:

1. Read the input sentence, which is a sequence of vectors, $x = (x_1, \dots, x_n)$ into a vector $c$, which is called a context vector;

   • Through the RNN, we would be computing the hidden state at time $t$ as $h_t = f(x_t, h_{t-1})$, where $f(\cdot)$ could be an LSTM;

   • The context vector is a nonlinear function of the encoder hidden states, $c = q(h_1, \dots, h_n)$. Early work used $c = h_n$, i.e., the last hidden state of the encoder was used as a context vector;

2. The decoder, then, predicts the next word given the context vector and all of the previously predicted words.

As mentioned, early work on NMT used the context vector $c$ only as an initializer of the decoder's hidden state. The intuition behind this is that the encoding RNN would find a good representation for the whole sentence and then, the translation would be done over this representation. This proved to work for shorter phrases but turned out to be a significant bottleneck for longer ones.

Another approach, which produces better results, is to build the context vector from all or from a subset of the encoder's hidden states, which are consulted throughout the translation process. This is referred to as an attention mechanism.

 (Adapted from [1]. Encoder (blue) and decoder (red) architecture using stacked RNNs to translate a source sequence A B C D into a target sequence X Y Z. Note that in this case, the context vector is simply the last hidden state of the encoder, which initializes the hidden state of the decoder.)

In terms of the attention mechanism, one can divide the approaches into two categories: global and local. The difference between them is based on whether the context vector is built based on all of the encoder's hidden states or just on a subset of them, in other words, if the attention is placed on the whole encoder or in just some of its units.

Global attention

In this approach,  the context vector is defined as a linear combination of all of the encoder's hidden states. Thus, at each time step, the decoder has a different context vector.

What varies at each time step are the weights that are used to compute the context vector. We are interested in weighing more heavily the parts of the encoder that have more to do with the word we are translating at that moment and weighing less the parts that have less to do. This process can be seen as an alignment: we are constantly aligning the current state of the decoder with the part of interest in the encoder.

In this model type, there is a variable-length alignment vector $a_t$, whose length equals the number of time steps on the source side. This alignment vector contains the weights that are going to be used to build the context vector and it is derived by comparing the current state of the decoder $h_t$ with each of the encoder states $\bar{h_s}$.

The score is a function that should measure the relation between the current decoder's hidden state $h_t$ with each encoder's hidden states $\bar{h_s}$. There are different possibilities for this score function. For instance, one could use a feedforward neural network, the inner product between $h_t$ and $h_s$, among other possibilities. Ideally, we would like to have some sort of interaction between these two hidden states in the score function, so an inner product-like function might be preferable over a feedforward neural network, for example.

Based on the alignment vectors $a_t$, the context vector $c_t$ for the decoder time step $t$ is given by

considering that the encoder has $n$ time steps ($n$ words to be translated). The alignment model is trained jointly with the translation model.

Local attention

The global attention mechanism has the drawback that we have to look over the whole encoder to compute the alignment vector. This process can be computationally expensive when we have longer input sequences such as paragraphs or whole documents. Thus, to circumvent this drawback, we can focus on just a subset of the encoder's units, i.e., focus only on a small window of context.

At each decoder time step $t$, the model generates an aligned position  $p_t$ . The context vector $c_t$ is, then, computed as a weighted average over the units within the window $[p_t - D, p_t + D]$, where the window length $2D$ is defined empirically. Therefore, the alignment vector $a_t$ always belong to $\mathbb{R}^{2D + 1}$ (contrasting to the global attention mechanism,  in which $a_t$ had variable length, depending on the source sequence).

There are different possibilities to define the aligned position $p_t$. The most straightforward one is to assume a monotonic alignment, i.e., assume that the source and target sequences are aligned and $p_t = t$. This is, of course, not always the case, but in general, there is some monotonicity between the source and target sequences.

Another possibility is the predictive alignment. In contrast to the monotonic alignment, now the model would predict the aligned position as:

Where $v_p$,  $W_p$ are model parameters to be learned and $S$ is the source sentence length. Note that $p_t \in [0, S]$ (due to the sigmoid) and is a real number. To favor points near the predicted $p_t$), a Gaussian distribution centered around $p_t$ is placed and the new alignment vector is defined as:

The standard deviation is empirically set to $\sigma = D/2$.

Making predictions

With the current decoder's hidden state $h_t$ and its corresponding context vector $c_t$ (which could be computed using global or local attention), a simple concatenation is employed, producing an attentional hidden state $\tilde{h_t}$ :

This attentional hidden state is then fed to the softmax layer to produce the predictive distribution.

The idea of using attention in NMT is interesting as it overcomes the bottleneck of encoding the whole sentence in a fixed-length vector. By using attention, information flows through the whole network and the encoder is freed from the burden of encoding the whole sentence into a vector and can now produce a context-disambiguated representation of the words. What is also stunning is the analysis of the alignment learned by the model. For instance, we note that the alignment is in a significant part monotonic, but some non-trivial alignments are idiosyncratic to certain languages.

 (Visualization of the learned alignment from [2] when translating from English to French.)

From NMT to multimodal emotion recognition

To adapt the ideas from NMT to the problem of multimodal emotion recognition using speech and text, I think that the first step would be to map the intrinsic similarities and differences between them.

I believe that the two key concepts from NMT are the encoder-decoder architecture and the use of context vectors bridging these two units. How shall this be adapted to the multimodal setting? We do have two RNNs, one for each modality, and they do work on their own, i.e., we can predict the emotions based solely on speech or solely on text. What we could do is impose some hierarchy between these two networks, resulting in a main and an auxiliary modality networks. The central role of the auxiliary modality network would be to provide the context vectors to the main modality network. The main modality network would, then, make its decision conditioned on its inputs and these context vectors. Thus, the analogies would be:

encoder/decoder ↔ auxiliary modality network/main modality network

How should we decide on which modality is the main and which is the auxiliary? I can think of arguments favoring both ways: the audio could be a context provider to the text or the text could be a context provider to the audio. I think that the audio could provide a better context to the text model because the text model on its own has better results than the audio model. Additionally, one could argue that by using the textual modality as our main one, the model as a whole focuses more on the meaning of the phrase and uses the learned characteristics of the audio just to help with context. The truth is that it might also not be such a good idea to artificially impose such a structure on the multimodal model.

To mimic the models from NMT, a first attempt could be to just initialize the hidden state of the main modality with the last hidden of the auxiliary modality. Indeed this was a limiting factor in the translation problem, but I think that we could just try it in the multimodal setting as it probably yields better results than with a single modality. A better approach would be to use attention mechanisms. Let the audio be the auxiliary modality and the text the main modality. From the audio RNN, we are interested in its hidden states $\bar{h_1}, \dots, \bar{h_n}$. On the other hand, on the text RNN, at each time step, we would input the vector corresponding to the current word and some combination of the previous state and a context vector. This context vector is calculated based on the hidden states of the audio RNN. The attention weights could be computed in the same way as in the NMT, via its alignment interpretation.

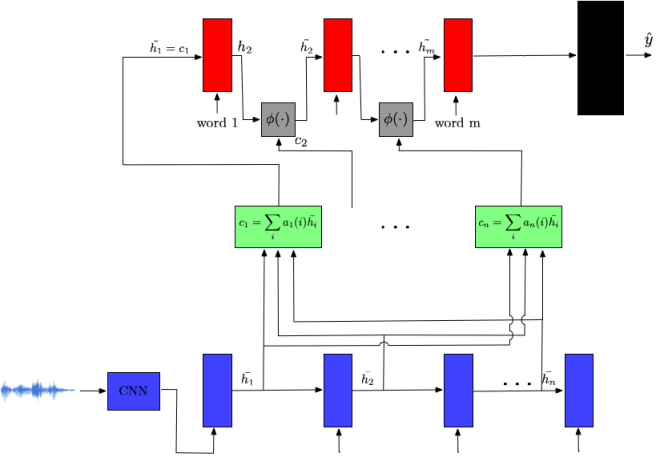
Proposed multimodal aproach using a global attention mechanism. At the bottom (blue) would be the audio model, at the top (red) the text model, in between (green) the attentional layer and in the end (black) a fully connected layer that outputs the label.

Let the audio model have $n$ RNN cells and the text model have $m$ RNN cells. We have the hidden states of the audio model as $\bar{h_1}, \dots, \bar{h_n}$. From them, we compute the output to the attention layer, which are the context vectors $c_1, \dots, c_m$, where $c_t = \sum_{i = 1}^{n} a_t(i) \bar{h_i}$. The alignment vectors $a_t$ are defined as:

Where $h_t$ corresponds to the hidden state at time step $t$ from the text model. We then need to compute $\tilde{h_t} = \phi(c_t, h_t)$, which is some function of the context vector and the hidden state of the text model (we still have to think about what would be a good $\phi(\cdot)$).

It might be interesting to check the learned alignment in this architecture. We could check the alignment vector for each word, meaning, if it indeed corresponds to the period of time that that word was being spoken.

Unlike the problem of translation, I think that in this setting, the alignment is always monotonic, so if we are afraid of the large number of new parameters introduced by the attention mechanism, we could use local attention with a fixed (small) window of context.

References

[1] M. T. Luong, H. Pham, C. D. Manning, "Effective approaches to attention-based neural machine translation", Conference on Empirical Methods in Natural Language Processing (EMNLP), 2015, pp. 1412–1421

[2] D. Bahdanau, K. H. Cho, Y. Bengio, "Neural machine translation by jointly learning to align and to translate", International Conference on Learning Representations (ICLR), 2015

[convertkit form=4006161]